At Buzzvil, we have an internal ads serving product called “BuzzAd”. Its main role is to serve ads and content articles in a highly optimized way. Optimization can come in lots of flavors. At their core, however, all such approaches use some scoring model to rank candidates. Take, for an example, a scenario where the HoneyScreen application must allocate K (<= N) items out of a pool of size N. Selecting K items at uniformly random is one way. Maybe, a better way is to choose the top K items based on their click through rates (CTR). When we have theoretically the best scoring model, deterministic approaches like sorting based on scores, however, still suffer from a few issues. Firstly, CTR and similar metrics can change over time. No one wants to repeatedly read the same set of ads or content articles. Conversely, changes in users’ interests can cause them to prefer items they did not like before. Secondly, deterministic approaches suffer from the cold start problem. If the content/ads pool is very big and sparse, deterministic approaches tend to be biased towards items already tried before. Specifically for our LockScreen platform, users can not actively choose to consume items other than what the app initially allocates. All that said, we would like some selection technique that has good properties of the deterministic approaches (i.e. sorting based on some metric) but also has an element of chance in it. Enter weighted random shuffling algorithms.

Overview

Weighted random shuffling algorithms are ways of permuting items in a sequence based on their given weights. When positions $latex 0, 1, .., i-1$ are already chosen, each remaining item has the probability of coming in position i equal to $latex P_i = w_i\ /\ (W_A\ -\ W_S) $, where $latex W_A$ is the sum of all weights and $latex W_S$ is the sum of weights already chosen. That is, WRS samples without replacement based on weights probabilities. Take for example an weights array [1,2,3]. The odds of each element coming in each position are as follows:   Just to give a few examples, WRS algorithms coupled with some scoring models can be used to solve problems such as:

1. In a big pool of ads and content articles, select K items that are most likely the top scoring K items.
2. Use as a valid strategy in multi-armed bandit settings.

All that said, how do we implement WRS?

Naive Approach

Its most naive and straightforward implementation can be thought of as repeatedly throwing a loaded dice. An weights array of length n is comparable to a loaded dice with n faces where the odds of face $latex i$ coming up is given by the $latex i\ th$ item in the array. Since WRS is a way of sampling without replacement, the loaded dice must reduce to $latex n-i$ faces after the first $latex i$ throws. In order to simulate WRS, we do the following at each throw,

1. Sample an integer $latex t\ in\ [0, T)$ at uniformly random.
2. Iterate over the weights array and select $latex i$ which satisfies $latex W[i-1] < T[i] <= W[i],\ where\ T[i] = T - sum\ of\ already\ chosen\ weights\ up\ to\ i$

The pseudocode is given below.

func throw_dice (arr_weights) {
  W <- sum(arr_weights)
  T <- RANDOM(0, W) // sample uniformly from [0, W)

  cumsum <- 0

  FOR i in 0..n-1, DO {

    IF T-cumsum <= arr_weigths[i], THEN
      RETURN arr_weights[i]

    cumsum += arr_weights[i]

  }
}

This naive approach obviously runs in$latex O(n^2)$. Repeatedly running this algorithm on a large $latex N$ is indeed expensive. Can we do better?

Binary Search Tree

Suppose instead you were given an weights array where element $latex i$ has a cumulative sum up to $latex w_i$. Can we do better? Yes. This is a perfect use case of binary search. You simply perform binary search on the weights array and find element $latex i$ such that $latex cum_w[i-1] < T <= cum_w[i]$. The catch, however, is that if you apply this technique to the original WRS problem, you need to find a way to update cumulative sums after drawing each sample that runs in time better than $latex O(N)$. Otherwise, this updating process accumulates to the overall running time of $latex O(N^2)$. Ideally, we would like to both search and update in $latex O(logN)$ and reduce the overall complexity to $latex O(NlogN)$. This can be achieved by using the data structure called the binary search tree(https://en.wikipedia.org/wiki/Binary_search_tree). Let’s delve into how this tree can be constructed and used to search and update in sub linear time.

Tree Construction

In order to represent and construct a binary search tree, you can surely write your own custom class and define its custom search and update methods. There is, however, a neat trick to represent a binary tree using a simple array. If our weights array is numbered from one instead of zero, every node $latex i$ of the binary search tree corresponds to the $latex i th$ item in the array and its left and right children to the $latex 2i\ th$ and $latex 2i+1\ th$ items in the array. Thus, by simply adding a dummy element to the head, we can represent our binary search tree. Additionally, each node of our tree contains tuples of form$latex (weight,\ total\_weight\_of\_subtree\_rooted\_at\_i)$. In order to compute those values, we conveniently set item 1 to the root of the tree and iterate over the array backwards, summing each node’s weight to its parent’s weight. That constructs our binary search tree.  

Search and Update

Once we construct our tree $latex T$, search and update operations become simple. For each sample, we perform the following operations in order.

1. Given an array of weights $latex w_1, w_2, …, w_n$, sample an integer $latex t$ in range $latex [0, W)$ at uniformly random. $latex W$ is the sum of all weights.
2. Start the search from the root and suppose we are currently at $latex node\ i$. If $latex r <= w_i$, then return information stored at $latex node\ i$. Otherwise, Update $latex r$ by subtracting $latex w_i$ from it and consider descending further down to the left subtree. If $latex r$ exceeds the total weight of this left subtree, we can cut this half of candidates and search the right subtree. Again update $latex r$ by subtracting the total weight of the left subtree $latex tw_{2i}$ if we are traversing down to the right subtree.
3. Once we find $latex node\ i$ that satisfies the search condition, update $latex w_i$ to 0 and subsequently update all its parents' weights by subtracting $latex w_i$.

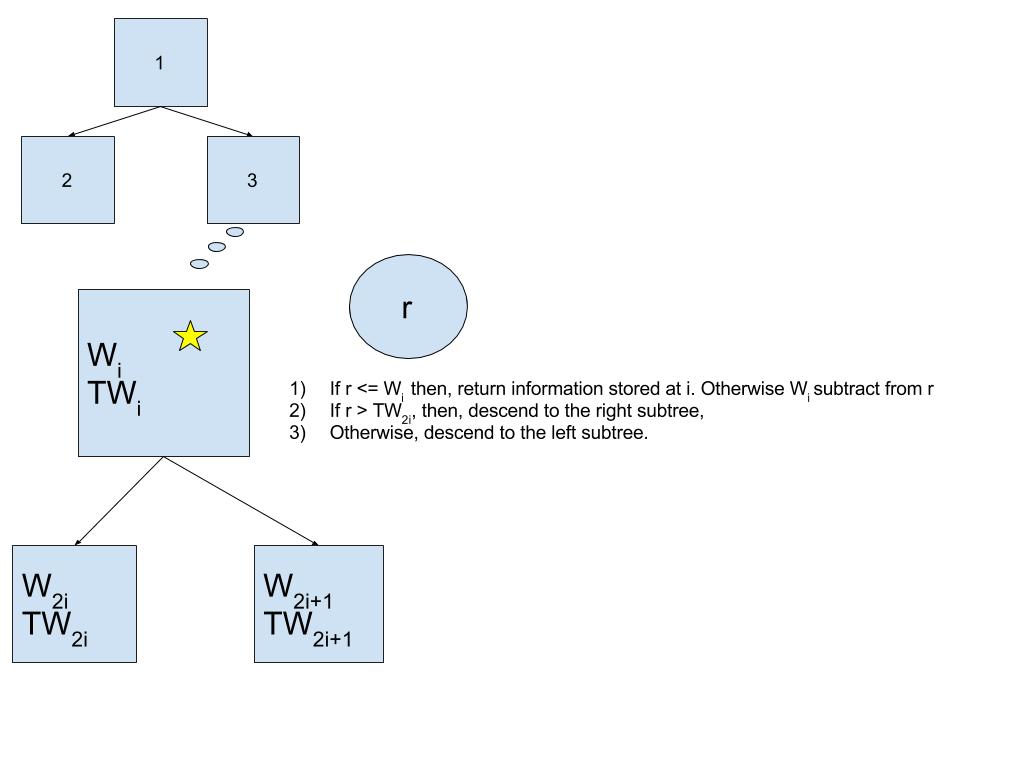  In the worst case, each search operation descends all the way from the root to a leaf node which takes time proportional to the height of tree, which is $latex O(logN)$. Each update operation must backtrack all the way to the root that takes $latex O(logN)$. 각각의 탐색과 업데이트는 $latex O(logN)$의 시간이 듭니다. 따라서 위 과정을 $latex N$번 반복하면 $latex O(NlogN)$의 시간이 들게 됩니다.

Optimization Tricks

In order to better tune our algorithm for data heavy production settings, we can make a few immediate observations and adjust accordingly.

1. A BST constructed this way is always a full binary tree for an odd N and almost full for an even N except for the lastly added node. Since the original order of an weights array is arbitrary, we can sort the array by weights in a descending order and position nodes with large weights near the root. This way, each search operation terminates closer to the root of a tree, improving the average running time of our algorithm.
2. Depending on what problem settings WRS is applied to, a given weights array may be updated in batches instead of in real time. This way, the tree construction part can be cached by popular cache frameworks like Redis or Memcache. This is another added bonus of representing our tree by a simple array. If your use case is an example of “sampling with replacement”, there are faster algorithms where the algorithms take linear time preprocessing but individual search and update operations run in constant time (alias method). Here, again the preprocessing part can benefit from the use of caches.

Wrapping it up…

At Buzzvil, we are building products that can withstand the load of size in the hundreds of thousands. To better serve our users and partners with personalized ads and content articles, we are constantly challenged to solve problems that require clever algorithms and data structures. Stay tuned on our blog as we continue to post our updates and solutions to interesting problems that come our way. And lastly but not least, if this is what interests you, don’t hesitate to contact us. We are hiring!